Dispersión de Rutherford
En el mundo actual, Dispersión de Rutherford es un tema que ha capturado la atención de millones de personas en todo el mundo. Desde su surgimiento, Dispersión de Rutherford ha generado debates, discusiones, y ha impactado de forma significativa en diversos ámbitos de la sociedad. Su relevancia ha trascendido fronteras y ha despertado un interés creciente en diferentes sectores, desde el ámbito académico y científico hasta el mundo del entretenimiento y la cultura popular. En este artículo, exploraremos a fondo el impacto de Dispersión de Rutherford y analizaremos sus efectos en la vida cotidiana de las personas. Asimismo, examinaremos su influencia en diferentes aspectos de la sociedad y reflexionaremos sobre su evolución a lo largo del tiempo.
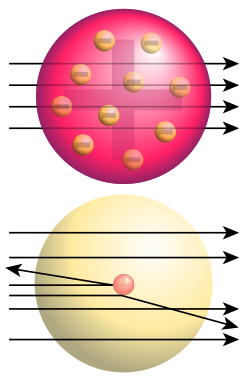
abajo: Resultados de Rutherford
La dispersión de Rutherford en mecánica clásica, también llamada dispersión de Couloumb, describe la dispersión de partículas eléctricamente cargadas al acercarse a un centro de dispersión que también debe estar cargado eléctricamente (experimento de Rutherford). La trayectoria resultante de las partículas dispersas es una hipérbola. A partir de la distribución espacial de las partículas dispersas se puede concluir de qué forma está estructurado el centro de dispersión. Con ayuda de esta teoría Hans Geiger, Ernest Marsden y Ernest Rutherford llegaron a la conclusión de que la carga positiva y la mayor parte de la masa del átomo debían estar concentradas en un pequeño espacio en el centro del átomo, al contrario del modelo de J.J. Thomson, en el que la carga positiva del átomo se distribuye de manera homogénea en una esfera (modelo atómico de Thomson). Al considerar los resultados, Rutherford dijo: «Esto es tan poco probable como si se disparara con un arma a una almohada de algodón, y que la bala rebote».
Este fenómeno físico fue explicado por Ernest Rutherford en 1911.
Fórmula de Rutherford

Con la denominada fórmula de dispersión de Rutherford se calcula la sección eficaz diferencial, la cual da la porción de partículas que llegan a .
en donde se describe la probabilidad de que las partículas dispersas incidan en un ángulo sólido después de ser desviadas en un ángulo .
En la fórmula se utiliza las siguientes constantes:
- Permitividad del vacío:
- Carga de la partícula dispersa:
- Carga del núcleo del átomo:
- Carga eléctrica elemental:
- Energía inicial de la partícula dispersa:
Véase también
 Portal:Física. Contenido relacionado con Física.
Portal:Física. Contenido relacionado con Física.- Teoría atómica
- Modelo atómico de Rutherford
Referencias
- ↑ Mecánica analítica. UNAM. 1 de enero de 2007. ISBN 9789703252275. Consultado el 15 de diciembre de 2015.
- ↑ Tipler, Paul Allen (1 de enero de 1994). Física moderna. Reverte. ISBN 9788429141863. Consultado el 15 de diciembre de 2015.








