Intersección (geometría)
Apariencia mover a la barra lateral ocultar
Punto de intersección de dos rectas
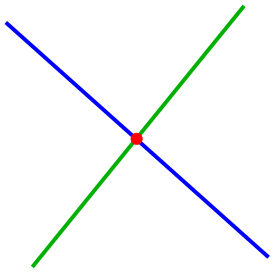
En geometría, una intersección es un punto, línea recta, curva, superficie o volumen, que es común a dos o más elementos (como líneas rectas, curvas, planos, superficies o volúmenes). El caso más simple en geometría euclidiana es la intersección de dos rectas distintas, que o bien es un punto o no existe si las líneas son paralelas.
La determinación de la intersección de planos o rectas definidos en un espacio dimensional superior, es una tarea simple de álgebra lineal, es decir, la solución de un sistema de ecuaciones lineales. Pero en general, la determinación de una intersección conduce a sistemas no lineales, que pueden ser solucionados por análisis numérico, por ejemplo, utilizando el método de Newton. Los problemas de intersección entre una línea y una sección cónica (círculo, elipse, parábola, etc.) o una cuádrica (esfera, cilindro, hiperboloide, etc.) conducen a ecuaciones de segundo grado que se pueden resolver fácilmente. Las intersecciones entre cuádricas (superficies de cuarto grado) llevan a ecuaciones cuárticas, que se pueden resolver algebraicamente.
En un plano
Véanse también: Plano y Espacio bidimensional.Dos rectas
Para la determinación del punto de intersección de dos líneas no paralelas
- a 1 x + b 1 y = c 1 , a 2 x + b 2 y = c 2 {\displaystyle a_{1}x+b_{1}y=c_{1},\ a_{2}x+b_{2}y=c_{2}}
se obtienen, a partir de la regla de Cramer o sustituyendo una variable, las coordenadas del punto de intersección ( x s , y s ) {\displaystyle (x_{s},y_{s})} :
x s = c 1 b 2 − c 2 b 1 a 1 b 2 − a 2 b 1 , y s = a 1 c 2 − a 2 c 1 a 1 b 2 − a 2 b 1 . {\displaystyle x_{s}={\frac {c_{1}b_{2}-c_{2}b_{1}}{a_{1}b_{2}-a_{2}b_{1}}},\quad y_{s}={\frac {a_{1}c_{2}-a_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}}.\ }
:
(Si a 1 b 2 − a 2 b 1 = 0 {\displaystyle a_{1}b_{2}-a_{2}b_{1}=0} las líneas son paralelas y estas fórmulas no se pueden usar porque implican dividir por 0).
las líneas son paralelas y estas fórmulas no se pueden usar porque implican dividir por 0).
Dos segmentos de recta
Intersección de dos segmentos de recta
Para dos segmentos no paralelos ( x 1 , y 1 ) , ( x 2 , y 2 ) {\displaystyle (x_{1},y_{1}),(x_{2},y_{2})} y ( x 3 , y 3 ) , ( x 4 , y 4 ) {\displaystyle (x_{3},y_{3}),(x_{4},y_{4})} , no necesariamente hay un punto de intersección (véase el diagrama), puesto que el punto de intersección ( x 0 , y 0 ) {\displaystyle (x_{0},y_{0})} de las rectas correspondientes puede no estar contenido en ambos segmentos. Para verificar la situación, se usa la representación paramétrica de las rectas:
( x ( s ) , y ( s ) ) = ( x 1 + s ( x 2 − x 1 ) , y 1 + s ( y 2 − y 1 ) ) , {\displaystyle (x(s),y(s))=(x_{1}+s(x_{2}-x_{1}),y_{1}+s(y_{2}-y_{1})),} ( x ( t ) , y ( t ) ) = ( x 3 + t ( x 4 − x 3 ) , y 3 + t ( y 4 − y 3 ) ) . {\displaystyle (x(t),y(t))=(x_{3}+t(x_{4}-x_{3}),y_{3}+t(y_{4}-y_{3})).}
y
(
x
3
,
y
3
)
,
(
x
4
,
y
4
)
{\displaystyle (x_{3},y_{3}),(x_{4},y_{4})}
, no necesariamente hay un punto de intersección (véase el diagrama), puesto que el punto de intersección
(
x
0
,
y
0
)
{\displaystyle (x_{0},y_{0})}
de las rectas correspondientes puede no estar contenido en ambos segmentos. Para verificar la situación, se usa la representación paramétrica de las rectas:
(
x
(
t
)
,
y
(
t
)
)
=
(
x
3
+
t
(
x
4
−
x
3
)
,
y
3
+
t
(
y
4
−
y
3
)
)
.
{\displaystyle (x(t),y(t))=(x_{3}+t(x_{4}-x_{3}),y_{3}+t(y_{4}-y_{3})).}
Los segmentos de línea se intersecan solo en un punto común ( x 0 , y 0 ) {\displaystyle (x_{0},y_{0})} de las líneas correspondientes si los parámetros correspondientes s 0 , t 0 {\displaystyle s_{0},t_{0}} cumplen la condición 0 ≤ s 0 , t 0 ≤ 1 {\displaystyle 0\leq s_{0},t_{0}\leq 1} . Los parámetros s 0 , t 0 {\displaystyle s_{0},t_{0}} son la solución del sistema lineal
s ( x 2 − x 1 ) − t ( x 4 − x 3 ) = x 3 − x 1 , {\displaystyle s(x_{2}-x_{1})-t(x_{4}-x_{3})=x_{3}-x_{1},} s ( y 2 − y 1 ) − t ( y 4 − y 3 ) = y 3 − y 1 . {\displaystyle s(y_{2}-y_{1})-t(y_{4}-y_{3})=y_{3}-y_{1}\ .}
cumplen la condición
0
≤
s
0
,
t
0
≤
1
{\displaystyle 0\leq s_{0},t_{0}\leq 1}
.
Los parámetros
s
0
,
t
0
{\displaystyle s_{0},t_{0}}
s
(
y
2
−
y
1
)
−
t
(
y
4
−
y
3
)
=
y
3
−
y
1
.
{\displaystyle s(y_{2}-y_{1})-t(y_{4}-y_{3})=y_{3}-y_{1}\ .}
Se puede resolver para s y t usando la regla de Cramer (véase más arriba). Si se cumple la condición 0 ≤ s 0 , t 0 ≤ 1 {\displaystyle 0\leq s_{0},t_{0}\leq 1} , se inserta s 0 {\displaystyle s_{0}} o t 0 {\displaystyle t_{0}} en la representación paramétrica correspondiente y se obtiene el punto de intersección ( x 0 , y 0 ) {\displaystyle (x_{0},y_{0})} .
o
t
0
{\displaystyle t_{0}}
en la representación paramétrica correspondiente y se obtiene el punto de intersección
(
x
0
,
y
0
)
{\displaystyle (x_{0},y_{0})}
Ejemplo: Para los segmentos de línea ( 1 , 1 ) , ( 3 , 2 ) {\displaystyle (1,1),(3,2)} y ( 1 , 4 ) , ( 2 , − 1 ) {\displaystyle (1,4),(2,-1)} se obtiene el sistema lineal
2 s − t = 0 {\displaystyle 2s-t=0} s + 5 t = 3 {\displaystyle s+5t=3}
y
(
1
,
4
)
,
(
2
,
−
1
)
{\displaystyle (1,4),(2,-1)}
se obtiene el sistema lineal
s
+
5
t
=
3
{\displaystyle s+5t=3}
y s 0 = 3 11 , t 0 = 6 11 {\displaystyle s_{0}={\tfrac {3}{11}},t_{0}={\tfrac {6}{11}}} . Esto significa que las líneas se cruzan en el punto ( 17 11 , 14 11 ) {\displaystyle ({\tfrac {17}{11}},{\tfrac {14}{11}})} .
. Esto significa que las líneas se cruzan en el punto
(
17
11
,
14
11
)
{\displaystyle ({\tfrac {17}{11}},{\tfrac {14}{11}})}
.
"Observación:" Teniendo en cuenta las rectas, en lugar de segmentos determinados por pares de puntos, cada condición 0 ≤ s 0 , t 0 ≤ 1 {\displaystyle 0\leq s_{0},t_{0}\leq 1} se puede descartar y el método produce el punto de intersección de las líneas (véase más arriba).
Intersección recta–circunferencia
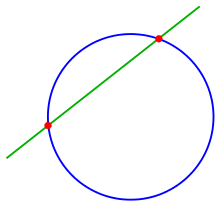
Una recta y una circunferencia
Para la intersección de
- recta a x + b y = c {\displaystyle ax+by=c} y circunferencia x 2 + y 2 = r 2 {\displaystyle x^{2}+y^{2}=r^{2}}
y 
se despeja la ecuación de la recta para x o para y, se sustituye en la ecuación de la circunferencia y se obtiene la solución (usando la fórmula de una ecuación cuadrática) ( x 1 , y 1 ) , ( x 2 , y 2 ) {\displaystyle (x_{1},y_{1}),(x_{2},y_{2})} con
x 1 / 2 = a c ± b r 2 ( a 2 + b 2 ) − c 2 a 2 + b 2 , {\displaystyle x_{1/2}={\frac {ac\pm b{\sqrt {r^{2}(a^{2}+b^{2})-c^{2}}}}{a^{2}+b^{2}}}\ ,} y 1 / 2 = b c ∓ a r 2 ( a 2 + b 2 ) − c 2 a 2 + b 2 , {\displaystyle y_{1/2}={\frac {bc\mp a{\sqrt {r^{2}(a^{2}+b^{2})-c^{2}}}}{a^{2}+b^{2}}}\ ,}
y
1
/
2
=
b
c
∓
a
r
2
(
a
2
+
b
2
)
−
c
2
a
2
+
b
2
,
{\displaystyle y_{1/2}={\frac {bc\mp a{\sqrt {r^{2}(a^{2}+b^{2})-c^{2}}}}{a^{2}+b^{2}}}\ ,}
si r 2 ( a 2 + b 2 ) − c 2 ≥ 0 . {\displaystyle r^{2}(a^{2}+b^{2})-c^{2}\geq 0\ .} Si esta condición se cumple, hay dos puntos de intersección; en este caso, la línea se llama recta secante del círculo, y el segmento de línea que conecta los puntos de intersección se denomina cuerda de la circunferencia.
Si esta condición se cumple, hay dos puntos de intersección; en este caso, la línea se llama Si r 2 ( a 2 + b 2 ) − c 2 = 0 {\displaystyle r^{2}(a^{2}+b^{2})-c^{2}=0} se mantiene, solo existe un punto de intersección y la línea es tangente al círculo. Si la desigualdad no se cumple, la línea no se cruza con el círculo.
se mantiene, solo existe un punto de intersección y la línea es tangente al círculo. Si la desigualdad no se cumple, la línea no se cruza con el círculo.
Si el punto medio de la circunferencia no es el origen, se puede hacer un desplazamiento del punto central al origen de coordenadas mediante un cambio de variable, cambio que se deshace una vez hallada la solución. La intersección de una línea y de una parábola o de una hipérbola se puede tratar de manera análoga.
Dos circunferencias
Intersección circunferencia–circunferencia
Intersección circunferencia–elipse
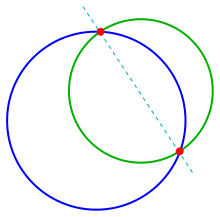
La determinación de los puntos de intersección de dos círculos
- ( x − x 1 ) 2 + ( y − y 1 ) 2 = r 1 2 , ( x − x 2 ) 2 + ( y − y 2 ) 2 = r 2 2 {\displaystyle (x-x_{1})^{2}+(y-y_{1})^{2}=r_{1}^{2},\ \quad (x-x_{2})^{2}+(y-y_{2})^{2}=r_{2}^{2}}
se puede reducir al caso anterior de intersección de una línea y un círculo. Al restar las dos ecuaciones dadas, se obtiene la ecuación lineal:
2 ( x 2 − x 1 ) x + 2 ( y 2 − y 1 ) y = r 1 2 − x 1 2 − y 1 2 − r 2 2 + x 2 2 + y 2 2 . {\displaystyle 2(x_{2}-x_{1})x+2(y_{2}-y_{1})y=r_{1}^{2}-x_{1}^{2}-y_{1}^{2}-r_{2}^{2}+x_{2}^{2}+y_{2}^{2}.}
La intersección del área de dos círculos define una figura denominada forma lenticular.
Dos secciones cónicas
El problema de la intersección de una elipse/hipérbola/parábola con otra sección cónica conduce a un sistema de ecuaciones cuadráticas, que puede resolverse en casos especiales fácilmente mediante la eliminación de una coordenada. Se pueden usar propiedades especiales de las secciones cónicas para obtener una solución. En general, los puntos de intersección pueden determinarse resolviendo la ecuación mediante una iteración de Newton. Si:
a) Ambas cónicas se dan implícitamente (mediante una ecuación); entonces se puede usar una iteración bidimensional de Newton. b) Una está dada implícitamente y la otra paramétricamente; entonces es posible utilizar una iteración de Newton de una dimensión (véase la siguiente sección).Dos curvas suaves
Intersección transversal de dos curvas
Dos curvas con intersección tangente (izquierda); y dos curvas tangentes entre sí (derecha)
Dos curvas en R 2 {\displaystyle \mathbb {R} ^{2}} (el espacio bidimensional), que son continuamente diferenciables (es decir, no presentan puntos de curvatura angulosos), tienen un punto de intersección, si poseen un punto del plano en común y tienen en este punto
a: tangentes distintas (intersección transversal), o b: una línea tangente en común y se cruzan entre sí (intersección tangente, véase el diagrama).
(el espacio bidimensional), que son continuamente diferenciables (es decir, no presentan puntos de curvatura angulosos), tienen un punto de intersección, si poseen un punto del plano en común y tienen en este punto
Si ambas curvas tienen un punto en común S y la tangente común en ese punto, pero no se cruzan entre sí, simplemente se están tocando en el punto S.
Debido a que las intersecciones tangentes aparecen con poca frecuencia y son difíciles de tratar, las siguientes consideraciones omiten este caso. Independientemente de esta circunstancia, se presuponen todas las condiciones de diferenciabilidad necesarias. La determinación de los puntos de intersección siempre conduce a una o dos ecuaciones no lineales, que pueden resolverse mediante la iteración de Newton. Una lista de los casos que aparecen a continuación:
Intersección de una curva paramétrica con una curva implícita
Intersección de dos curvas implícitas
- Si ambas curvas están explícitamente dadas: y = f 1 ( x ) , y = f 2 ( x ) {\displaystyle y=f_{1}(x),\ y=f_{2}(x)} , igualarlas produce la ecuación
, igualarlas produce la ecuación
- Si ambas curvas están dadas paramétricamente: C 1 : ( x 1 ( t ) , y 1 ( t ) ) , C 2 : ( x 2 ( s ) , y 2 ( s ) ) . {\displaystyle C_{1}:(x_{1}(t),y_{1}(t)),\ C_{2}:(x_{2}(s),y_{2}(s)).}
- Si una curva es paramétrica y la otra implícita: C 1 : ( x 1 ( t ) , y 1 ( t ) ) , C 2 : f ( x , y ) = 0. {\displaystyle C_{1}:(x_{1}(t),y_{1}(t)),\ C_{2}:f(x,y)=0.}
en la ecuación
f
(
x
,
y
)
=
0
{\displaystyle f(x,y)=0}
de la curva
C
2
{\displaystyle C_{2}}
y se obtiene la ecuación:
f
(
x
(
t
)
,
y
(
t
)
)
=
0
.
{\displaystyle f(x(t),y(t))=0\ .}
- Si ambas curvas están implícitamente dadas: C 1 : f 1 ( x , y ) = 0 , C 2 : f 2 ( x , y ) = 0. {\displaystyle C_{1}:f_{1}(x,y)=0,\ C_{2}:f_{2}(x,y)=0.}
Cualquier iteración de Newton necesita valores iniciales convenientes, que pueden derivarse mediante una visualización de ambas curvas. Una curva dada paramétrica o explícitamente puede visualizarse fácilmente, porque para cualquier parámetro t o x respectivamente es fácil calcular el punto correspondiente. Para curvas dadas implícitamente esta tarea no es tan fácil. En este caso, debe determinarse un punto de la curva con la ayuda de los valores iniciales y un método de iteración.
Ejemplos:
1: C 1 : ( t , t 3 ) {\displaystyle C_{1}:(t,t^{3})} y la circunferencia C 2 : ( x − 1 ) 2 + ( y − 1 ) 2 − 10 = 0 {\displaystyle C_{2}:(x-1)^{2}+(y-1)^{2}-10=0} (véase diagrama). Debe efectuarse la iteración de Newton t n + 1 := t n − f ( t n ) f ′ ( t n ) {\displaystyle t_{n+1}:=t_{n}-{\frac {f(t_{n})}{f'(t_{n})}}} para la función f ( t ) = ( t − 1 ) 2 + ( t 3 − 1 ) 2 − 10 {\displaystyle f(t)=(t-1)^{2}+(t^{3}-1)^{2}-10} . Como valores iniciales pueden elegirse -1 y 1.5. Los puntos de intersección son: (-1.1073, -1.3578), (1.6011, 4.1046) 2: C 1 : f 1 ( x , y ) = x 4 + y 4 − 1 = 0 , {\displaystyle C_{1}:f_{1}(x,y)=x^{4}+y^{4}-1=0,} C 2 : f 2 ( x , y ) = ( x − 0.5 ) 2 + ( y − 0.5 ) 2 − 1 = 0 {\displaystyle C_{2}:f_{2}(x,y)=(x-0.5)^{2}+(y-0.5)^{2}-1=0} (véase el diagrama). La iteración de Newton se debe realizar sobre ( x n + 1 y n + 1 ) = ( x n + δ x y n + δ y ) {\displaystyle {x_{n+1} \choose y_{n+1}}={x_{n}+\delta _{x} \choose y_{n}+\delta _{y}}} , donde ( δ x δ y ) {\displaystyle {\delta _{x} \choose \delta _{y}}} es la solución del sistema lineal ( ∂ f 1 ∂ x ∂ f 1 ∂ y ∂ f 2 ∂ x ∂ f 2 ∂ y ) ( δ x δ y ) = ( − f 1 − f 2 ) {\displaystyle {\begin{pmatrix}{\frac {\partial f_{1}}{\partial x}}&{\frac {\partial f_{1}}{\partial y}}\\{\frac {\partial f_{2}}{\partial x}}&{\frac {\partial f_{2}}{\partial y}}\end{pmatrix}}{\delta _{x} \choose \delta _{y}}={-f_{1} \choose -f_{2}}} en el punto ( x n , y n ) {\displaystyle (x_{n},y_{n})} . Como valores de iniciales se pueden elegir (-0.5, 1) y (1, -0.5). El sistema lineal puede ser resuelto por la regla de Cramer. Los puntos de intersección son (-0.3686, 0.9953) y (0.9953, -0.3686).
y la circunferencia
C
2
:
(
x
−
1
)
2
+
(
y
−
1
)
2
−
10
=
0
{\displaystyle C_{2}:(x-1)^{2}+(y-1)^{2}-10=0}
(véase diagrama).
Debe efectuarse la iteración de Newton
t
n
+
1
:=
t
n
−
f
(
t
n
)
f
′
(
t
n
)
{\displaystyle t_{n+1}:=t_{n}-{\frac {f(t_{n})}{f'(t_{n})}}}
para la función
f
(
t
)
=
(
t
−
1
)
2
+
(
t
3
−
1
)
2
−
10
{\displaystyle f(t)=(t-1)^{2}+(t^{3}-1)^{2}-10}
. Como valores iniciales pueden elegirse -1 y 1.5.
Los puntos de intersección son: (-1.1073, -1.3578), (1.6011, 4.1046)
2:
C
1
:
f
1
(
x
,
y
)
=
x
4
+
y
4
−
1
=
0
,
{\displaystyle C_{1}:f_{1}(x,y)=x^{4}+y^{4}-1=0,}
C
2
:
f
2
(
x
,
y
)
=
(
x
−
0.5
)
2
+
(
y
−
0.5
)
2
−
1
=
0
{\displaystyle C_{2}:f_{2}(x,y)=(x-0.5)^{2}+(y-0.5)^{2}-1=0}
(véase el diagrama).
La iteración de Newton se debe realizar sobre
(
x
n
+
1
y
n
+
1
)
=
(
x
n
+
δ
x
y
n
+
δ
y
)
{\displaystyle {x_{n+1} \choose y_{n+1}}={x_{n}+\delta _{x} \choose y_{n}+\delta _{y}}}
, donde
(
δ
x
δ
y
)
{\displaystyle {\delta _{x} \choose \delta _{y}}}
es la solución del sistema lineal
(
∂
f
1
∂
x
∂
f
1
∂
y
∂
f
2
∂
x
∂
f
2
∂
y
)
(
δ
x
δ
y
)
=
(
−
f
1
−
f
2
)
{\displaystyle {\begin{pmatrix}{\frac {\partial f_{1}}{\partial x}}&{\frac {\partial f_{1}}{\partial y}}\\{\frac {\partial f_{2}}{\partial x}}&{\frac {\partial f_{2}}{\partial y}}\end{pmatrix}}{\delta _{x} \choose \delta _{y}}={-f_{1} \choose -f_{2}}}
en el punto
(
x
n
,
y
n
)
{\displaystyle (x_{n},y_{n})}
. Como valores de iniciales se pueden elegir (-0.5, 1) y (1, -0.5).
El sistema lineal puede ser resuelto por la regla de Cramer.
Los puntos de intersección son (-0.3686, 0.9953) y (0.9953, -0.3686).
Dos polígonos
Intersección de dos polígonos: prueba de la ventana
Si se quieren determinar los puntos de intersección de dos polígonos, se puede verificar la intersección de cualquier par de segmentos de línea de los polígonos (véase arriba). Para polígonos con muchos segmentos, este método requiere bastante tiempo. En la práctica, se acelera el algoritmo de intersección mediante el uso de "pruebas de ventana". En este caso, se dividen los polígonos en pequeños subpolígonos y se determina la ventana más pequeña (rectángulo con lados paralelos a los ejes de coordenadas) para cualquier subpolígono. Antes de comenzar la determinación que consume mucho tiempo del punto de intersección de dos segmentos de línea, se comprueba si cualquier par de ventanas tiene puntos comunes.
En el espacio (tres dimensiones)
Véase también: Espacio tridimensionalEn el espacio tridimensional, también pueden existir puntos de intersección (puntos comunes) entre las curvas y las superficies. En las siguientes secciones se considera la intersección transversal solamente.
Una recta y un plano
Intersección de una recta y un plano
En tres dimensiones, la intersección de una recta y un plano en posición general es un punto.
Comúnmente, una línea en el espacio se representa paramétricamente ( x ( t ) , y ( t ) , z ( t ) ) {\displaystyle (x(t),y(t),z(t))} , así como un plano mediante una ecuación del tipo
a x + b y + c z = d {\displaystyle ax+by+cz=d}
, así como un plano mediante una ecuación del tipo
Al sustituir los parámetros en la ecuación, se obtiene la ecuación lineal
a x ( t ) + b y ( t ) + c z ( t ) = d , {\displaystyle ax(t)+by(t)+cz(t)=d\ ,}
con el parámetro t 0 {\displaystyle t_{0}} correspondiente al punto de intersección ( x ( t 0 ) , y ( t 0 ) , z ( t 0 ) ) {\displaystyle (x(t_{0}),y(t_{0}),z(t_{0}))} .
.
Si la ecuación lineal no tiene solución, la línea yace en el plano o es paralela a ella.
Tres planos
Si una recta está definida por dos planos de intersección ε i : n → i ⋅ x → = d i , i = 1 , 2 {\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2} y debe cruzarse con un tercer plano ε 3 : n → 3 ⋅ x → = d 3 {\displaystyle \varepsilon _{3}:\ {\vec {n}}_{3}\cdot {\vec {x}}=d_{3}} , se debe evaluar el punto de intersección común de los tres planos.
y debe cruzarse con un tercer plano
ε
3
:
n
→
3
⋅
x
→
=
d
3
{\displaystyle \varepsilon _{3}:\ {\vec {n}}_{3}\cdot {\vec {x}}=d_{3}}
, se debe evaluar el punto de intersección común de los tres planos.
Tres planos ε i : n → i ⋅ x → = d i , i = 1 , 2 , 3 {\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2,3} con vectores normales linealmente independientes n → 1 , n → 2 , n → 3 {\displaystyle {\vec {n}}_{1},{\vec {n}}_{2},{\vec {n}}_{3}} tienen el punto de intersección
p → 0 = d 1 ( n → 2 × n → 3 ) + d 2 ( n → 3 × n → 1 ) + d 3 ( n → 1 × n → 2 ) n → 1 ⋅ ( n → 2 × n → 3 ) . {\displaystyle {\vec {p}}_{0}={\frac {d_{1}({\vec {n}}_{2}\times {\vec {n}}_{3})+d_{2}({\vec {n}}_{3}\times {\vec {n}}_{1})+d_{3}({\vec {n}}_{1}\times {\vec {n}}_{2})}{{\vec {n}}_{1}\cdot ({\vec {n}}_{2}\times {\vec {n}}_{3})}}\ .}
con vectores normales linealmente independientes
n
→
1
,
n
→
2
,
n
→
3
{\displaystyle {\vec {n}}_{1},{\vec {n}}_{2},{\vec {n}}_{3}}
tienen el punto de intersección
Para la prueba se debe establecer n → i ⋅ p → 0 = d i , i = 1 , 2 , 3 , {\displaystyle {\vec {n}}_{i}\cdot {\vec {p}}_{0}=d_{i},\ i=1,2,3,} usando las reglas de un producto mixto. Si el producto escalar triple es igual a 0, entonces los planos no poseen una intersección triple o es una recta (o un plano, si los tres planos son iguales).
usando las reglas de un Una curva y una superficie
Intersección de una curva
(
t
,
t
2
,
t
3
)
{\displaystyle (t,t^{2},t^{3})}
con una superficie
x
4
+
y
4
+
z
4
=
1
{\displaystyle x^{4}+y^{4}+z^{4}=1}
con una superficie
x
4
+
y
4
+
z
4
=
1
{\displaystyle x^{4}+y^{4}+z^{4}=1}
Análogamente al caso plano, los casos siguientes conducen a sistemas no lineales, que se pueden resolver utilizando una iteración de Newton de 1 o 3 dimensiones.
- Curva paramétrica C : ( x ( t ) , y ( t ) , z ( t ) {\displaystyle C:(x(t),y(t),z(t)} y
y
- Curva paramétrica C : ( x ( t ) , y ( t ) , z ( t ) {\displaystyle C:(x(t),y(t),z(t)} y
Ejemplo:
Curva paramétrica C : ( t , t 2 , t 3 ) {\displaystyle C:(t,t^{2},t^{3})} y superficie implícita S : x 4 + y 4 + z 4 − 1 = 0 {\displaystyle S:x^{4}+y^{4}+z^{4}-1=0} (imagen s). Los puntos de intersección son: (-0.8587, 0.7374, -0.6332), (0.8587, 0.7374, 0.6332).
y
superficie implícita
S
:
x
4
+
y
4
+
z
4
−
1
=
0
{\displaystyle S:x^{4}+y^{4}+z^{4}-1=0}
(imagen s).
Los puntos de intersección son: (-0.8587, 0.7374, -0.6332), (0.8587, 0.7374, 0.6332).
Una intersección de recta y esfera es un caso especial simple.
Como en el caso de una recta y un plano, la intersección de una curva y una superficie en posición general consiste en puntos discretos, pero una curva puede estar parcial o totalmente contenida en una superficie.
Una recta y un poliedro
Dos superficies
Dos superficies intersecantes transversalmente dan una intersección curva. El caso más simple es la recta de intersección de dos planos no paralelos.
Véase también
- Ceviana
- Intersección de conjuntos
- Intersección de segmentos de recta
- Intersección de dos rectas
- Intersección de dos planos
- Geometría computacional
- Ecuación de primer grado
Referencias
- ↑ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 17
- ↑ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 33
- ↑ Erich Hartmann: CDKG: Computerunterstützte Darstellende und Konstruktive Geometrie. Lecture notes, TU Darmstadt, 1997, p. 79 (PDF; 3,4 MB)
- ↑ Erich Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN. Lecture notes, Technische Universität Darmstadt, October 2003, p. 93