Mediana (geometría)

Apariencia mover a la barra lateral ocultar

Las transversales de gravedad de un triángulo (líneas rojas) se cortan en el baricentro del mismo.

En geometría, la mediana, media o transversal de gravedad de un triángulo, es el segmento de recta que une un vértice con el punto medio del lado opuesto.

Propiedades

Las transversales de gravedad de un triángulo (líneas verdes) se cortan en el baricentro (centro de gravedad).

Para las medianas se anotan las siguientes propiedades:

Cada mediana divide al triángulo en dos triángulos, siendo lado común de ellos; dichos triángulos, en general, no son congruentes; pero sí equivalentes, de igual área, por ejemplo para el caso de la mediana AI (véase la figura) dichas regiones son los dos triángulos ΔABI y ΔACI de igual área.
Las tres medianas se intersecan en un único punto, llamado baricentro, centroide o centro de gravedad.
Dos tercios de la longitud de cada mediana están entre el vértice y el baricentro, mientras que el tercio restante está entre el baricentro y el punto medio del lado opuesto.
Para cualquier triángulo rectilíneo con lados a , b , c {\displaystyle a,b,c} $a,b,c$ , medianas m a , m b , m c {\displaystyle m_{a},m_{b},m_{c}} $m_{a},m_{b},m_{c}$ y perímetro p {\displaystyle p} $p$ , se cumple la siguiente desigualdad:

3 4 p < ( m a + m b + m c ) < 3 2 p {\displaystyle {\frac {3}{4}}p<\left(m_{a}+m_{b}+m_{c}\right)<{\frac {3}{2}}p} ${\frac {3}{4}}p<\left(m_{a}+m_{b}+m_{c}\right)<{\frac {3}{2}}p$

Para cualquier triángulo con lados a , b , c {\displaystyle a,b,c} $a,b,c$ y medianas m a , m b , m c {\displaystyle m_{a},m_{b},m_{c}} $m_{a},m_{b},m_{c}$ , p r a {\displaystyle pr_{a}} $pr_{a}$ la proyección de m a {\displaystyle m_{a}} $m_{a}$ sobre a, los elementos indicados verifican las siguientes ecuaciones:

m a 2 + m b 2 + m c 2 = 3 4 ( a 2 + b 2 + c 2 ) . {\displaystyle m_{a}^{2}+m_{b}^{2}+m_{c}^{2}\;=\;{\tfrac {3}{4}}\;(a^{2}+b^{2}+c^{2}).}

m_{a}^{2}+m_{b}^{2}+m_{c}^{2}\;=\;{\tfrac {3}{4}}\;(a^{2}+b^{2}+c^{2}).

b 2 + c 2 = 2 m a 2 + a 2 2 {\displaystyle b^{2}+c^{2}=2m_{a}^{2}+{\frac {a^{2}}{2}}}

b^{2}+c^{2}=2m_{a}^{2}+{\frac {a^{2}}{2}}

m a = 1 2 2 b 2 + 2 c 2 − a 2 {\displaystyle m_{a}={\frac {1}{2}}{\sqrt {2b^{2}+2c^{2}-a^{2}}}}

m_{a}={\frac {1}{2}}{\sqrt {2b^{2}+2c^{2}-a^{2}}}

2 a × p r a = b 2 − c 2 {\displaystyle 2a\times pr_{a}=b^{2}-c^{2}}

2a\times pr_{a}=b^{2}-c^{2}

Relación con el centro de gravedad

Cada una de las tres medianas de un triángulo pasa por el centroide del mismo, el cual es coincidente con el centro de gravedad de un objeto con forma de triángulo (si éste es de densidad uniforme). Así, dicho objeto estaría en equilibrio en cualquier transversal de gravedad (línea que pase a través del centro de gravedad ), Las medianas son solo tres transversales de gravedad, del haz infinito de transversales de gravedad del triángulo.

Teorema de la mediana

fig. m1: Esquema con áreas → ( a 2 + b 2 = 1 2 c 2 + 2 M 2 {\displaystyle {\scriptstyle {\color {Red}a^{2}}\;+\;{\color {Orange}b^{2}}\;=\;{\color {Blue}{\frac {1}{2}}\;c^{2}}\;+\;{\color {OliveGreen}2\;M^{2}}}}

{\scriptstyle {\color {Red}a^{2}}\;+\;{\color {Orange}b^{2}}\;=\;{\color {Blue}{\frac {1}{2}}\;c^{2}}\;+\;{\color {OliveGreen}2\;M^{2}}}

En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es una proposición que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.

Teorema de Apolonio (teorema de la mediana)

Para todo triángulo la suma de los cuadrados de dos lados cualesquiera, es igual a la mitad del cuadrado del tercer lado más el doble del cuadrado de su mediana correspondiente.

Apolonio de Perga

Para cualquier triángulo ΔABC (véase fig. m1), si mc es la mediana correspondiente al lado c, donde AP = PB = ½ c, entonces :

a 2 + b 2 = 1 2 c 2 + 2 m c 2 {\displaystyle a^{2}+b^{2}={\frac {1}{2}}\;c^{2}+2\;m_{c}^{2}} $a^{2}+b^{2}={\frac {1}{2}}\;c^{2}+2\;m_{c}^{2}$

Fórmulas algebraicas de medianas en función de lados

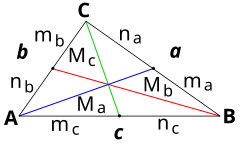
Del teorema de Apolonio, también llamado "teorema de la mediana", pueden deducirse varias fórmulas prácticas (válidas para cualquier triángulo). Estas permiten calcular a partir del conocimiento de tres elementos, a un cuarto elemento desconocido, (los elementos en cuestión son lados y medianas). La siguiente tabla muestra un resumen de las mismas (con notación acorde a la figura de la propia tabla) :

Triángulos — Medianas ( fórmulas prácticas II )

M a = 1 2 2 ( b 2 + c 2 ) − a 2 {\displaystyle M_{a}={\frac {1}{2}}{\sqrt {2\left(b^{2}+c^{2}\right)-a^{2}}}}

M_{a}={\frac {1}{2}}{\sqrt {2\left(b^{2}+c^{2}\right)-a^{2}}}

M b = 1 2 2 ( a 2 + c 2 ) − b 2 {\displaystyle M_{b}={\frac {1}{2}}{\sqrt {2\left(a^{2}+c^{2}\right)-b^{2}}}}

M_{b}={\frac {1}{2}}{\sqrt {2\left(a^{2}+c^{2}\right)-b^{2}}}

M c = 1 2 2 ( a 2 + b 2 ) − c 2 {\displaystyle M_{c}={\frac {1}{2}}{\sqrt {2\left(a^{2}+b^{2}\right)-c^{2}}}}

M_{c}={\frac {1}{2}}{\sqrt {2\left(a^{2}+b^{2}\right)-c^{2}}}

a = 2 ( b 2 + c 2 ) − 4 M a 2 {\displaystyle a={\sqrt {2\left(b^{2}+c^{2}\right)-4M_{a}^{2}}}}

a={\sqrt {2\left(b^{2}+c^{2}\right)-4M_{a}^{2}}}

b = a 2 2 − c 2 + 2 M a 2 {\displaystyle b={\sqrt {{\frac {a^{2}}{2}}-c^{2}+2M_{a}^{2}}}}

b={\sqrt {{\frac {a^{2}}{2}}-c^{2}+2M_{a}^{2}}}

c = a 2 2 − b 2 + 2 M a 2 {\displaystyle c={\sqrt {{\frac {a^{2}}{2}}-b^{2}+2M_{a}^{2}}}}

c={\sqrt {{\frac {a^{2}}{2}}-b^{2}+2M_{a}^{2}}}

a = b 2 2 − c 2 + 2 M b 2 {\displaystyle a={\sqrt {{\frac {b^{2}}{2}}-c^{2}+2M_{b}^{2}}}}

a={\sqrt {{\frac {b^{2}}{2}}-c^{2}+2M_{b}^{2}}}

b = 2 ( a 2 + c 2 ) − 4 M b 2 {\displaystyle b={\sqrt {2\left(a^{2}+c^{2}\right)-4M_{b}^{2}}}}

b={\sqrt {2\left(a^{2}+c^{2}\right)-4M_{b}^{2}}}

c = − a 2 + b 2 2 + 2 M b 2 {\displaystyle c={\sqrt {-a^{2}+{\frac {b^{2}}{2}}+2M_{b}^{2}}}}

c={\sqrt {-a^{2}+{\frac {b^{2}}{2}}+2M_{b}^{2}}}

a = − b 2 + c 2 2 + 2 M c 2 {\displaystyle a={\sqrt {-b^{2}+{\frac {c^{2}}{2}}+2M_{c}^{2}}}}

a={\sqrt {-b^{2}+{\frac {c^{2}}{2}}+2M_{c}^{2}}}

b = − a 2 + c 2 2 + 2 M c 2 {\displaystyle b={\sqrt {-a^{2}+{\frac {c^{2}}{2}}+2M_{c}^{2}}}}

b={\sqrt {-a^{2}+{\frac {c^{2}}{2}}+2M_{c}^{2}}}

c = 2 ( a 2 + b 2 ) − 4 M c 2 {\displaystyle c={\sqrt {2\left(a^{2}+b^{2}\right)-4M_{c}^{2}}}}

c={\sqrt {2\left(a^{2}+b^{2}\right)-4M_{c}^{2}}}

( Lados: a, b y c ) — ( Medianas: Ma, Mb y Mc ) — ( Semilados: ma=na = ½ a , mb=nb = ½ b y mc=nc = ½ c ).

En el triángulo isósceles

m a = h a = b A = 1 2 4 b 2 − a 2 {\displaystyle m_{a}=h_{a}=b_{A}={\frac {1}{2}}{\sqrt {4b^{2}-a^{2}}}}

m_{a}=h_{a}=b_{A}={\frac {1}{2}}{\sqrt {4b^{2}-a^{2}}}

; m b = m c = 1 2 2 a 2 + b 2 {\displaystyle m_{b}=m_{c}={\frac {1}{2}}{\sqrt {2a^{2}+b^{2}}}}

m_{b}=m_{c}={\frac {1}{2}}{\sqrt {2a^{2}+b^{2}}}

En el triángulo rectángulo

m a = a 2 {\displaystyle m_{a}={\frac {a}{2}}}

m_{a}={\frac {a}{2}}

m b = 1 2 4 a 2 − 3 b 2 = 1 2 a 2 + 3 c 2 = 1 2 b 2 + 4 c 2 {\displaystyle m_{b}={\frac {1}{2}}{\sqrt {4a^{2}-3b^{2}}}={\frac {1}{2}}{\sqrt {a^{2}+3c^{2}}}={\frac {1}{2}}{\sqrt {b^{2}+4c^{2}}}}

m_{b}={\frac {1}{2}}{\sqrt {4a^{2}-3b^{2}}}={\frac {1}{2}}{\sqrt {a^{2}+3c^{2}}}={\frac {1}{2}}{\sqrt {b^{2}+4c^{2}}}

m c = 1 2 4 a 2 − 3 c 2 = 1 2 a 2 + 3 b 2 = 1 2 4 b 2 + c 2 {\displaystyle m_{c}={\frac {1}{2}}{\sqrt {4a^{2}-3c^{2}}}={\frac {1}{2}}{\sqrt {a^{2}+3b^{2}}}={\frac {1}{2}}{\sqrt {4b^{2}+c^{2}}}}

m_{c}={\frac {1}{2}}{\sqrt {4a^{2}-3c^{2}}}={\frac {1}{2}}{\sqrt {a^{2}+3b^{2}}}={\frac {1}{2}}{\sqrt {4b^{2}+c^{2}}}

Triángulo medial

Se conoce con el nombre de triángulo medial respecto a otro triángulo al que tiene como vértices los puntos medios de un triángulo cualquiera dado.

Proposiciones

Los lados de un triángulo medial son las bases medias de un triángulo dado.
El baricentro de un triángulo coincide con el baricentro del triángulo medial.
El área de un triángulo medial es 1/4 del área del triángulo original.
Un triángulo medial es semejante al triángulo inicial
En cualquier triángulo isósceles la mediana correspondiente a la base es a la vez altura y bisectriz y es parte de la línea mediatriz de tal base.

Mediana de un trapecio

En cualquier trapecio, se llama mediana al segmento que une los puntos medios de los lados no paralelos. Recibe también el nombre de paralela media. En algunos países (e.g. Chile) a la paralela media se le llama mediana, mientras que el concepto de mediana se llama allí transversal de gravedad.

La mediana del trapecio es paralela a las bases e igual a la semisuma de las mismas.

Véase también

Triángulo
Ceviana
Bisectriz
Mediatriz
Altura (geometría)
Teorema de Stewart
Teorema de Apolonio (Teorema de la mediana).
Ley del paralelogramo.

Referencias

↑ Guia de problemas Matemática I.Reinaldo Giudici E..Ed:Equinoccio. Venezuela.
↑ Michel Helfgott: Geometria moderna
↑ M. García Ardura: Problemas gráficos y numéricos de geometría editado en España, novena edición
↑ a b Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp. 86-87.
↑ M. García Ardura. Problemas gráficos y numéricos de Geometría. Decimocuarta edición, Madrid
↑ Déplanche, Y.,Diccio fórmulas, 1996, Edunsa (publ.), "Medianas de un triángulo" pág. 25. , isbn=9788477471196
↑ La altura de la base coincide con la mediana y la bisectriz de la misma, en un triángulo isóseceles.
↑ Hay una hermosa simetría de las dos últimas fórmulas.
↑ Alencar. Exercícios de geometria plana
↑ Jimmy García. Resumen teórico de matemáticas y Ciencias. Fondo editorial Rodó. Lima (2013)
↑ César A. Trejo/ Jorge E. Bosch «Matemática moderna /Primer curso» Eudeba, Buenos Aires (1966)
↑ estrada/ sánchez Geometría plana. Editorial Pueblo y Educación, La Habana (2010)
↑ «Capítulo 13: Figuras Geométricas». Matemática Para Nacional, Texto preparación Prueba de Transición Matemática (6ta edición). Chile: Moraleja. 2021. p. 328. ISBN 978-956-7275-27-4.
↑ Proposición en cualquier manual de geometría plana

Enlaces externos

Weisstein, Eric W. «Triangle Median». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.