Pequeño icosicosidodecaedro retrorromo

En el amplio espectro de Pequeño icosicosidodecaedro retrorromo, se pueden encontrar una gran variedad de temas, enfoques y perspectivas. Tanto si se trata de explorar la vida y obra de un personaje histórico, analizar los desafíos actuales en un determinado ámbito o reflexionar sobre el impacto de una fecha significativa, Pequeño icosicosidodecaedro retrorromo nos invita a sumergirnos en un universo de posibilidades. A través de este artículo, nos adentraremos en un viaje fascinante que nos permitirá descubrir, aprender y reflexionar sobre Pequeño icosicosidodecaedro retrorromo desde diversas miradas.

Pequeño icosicosidodecaedro retrorromo

Modelo 3D
Tipo poliedro uniforme, poliedro no convexo y poliedro romo Modificar el valor en Wikidata
Forma de las caras triángulo equilátero (80, 100)
pentagrama (12) Modificar el valor en Wikidata
Configuración de vértices hexágono Modificar el valor en Wikidata
Símbolo de Schläfli ß{3/2,5} Modificar el valor en Wikidata
Dual pequeño hexecontaedro hexagrámico Modificar el valor en Wikidata
Elementos
Vértices 60
Aristas 180
Caras 112 Modificar el valor en Wikidata
Más información
MathWorld SmallRetrosnubIcosicosidodecahedron Modificar el valor en Wikidata

En geometría, el pequeño icosicosidodecaedro retrorromo (también conocido como disicosidodecaedro retrorromo, pequeño icosicosidodecaedro retrorromo invertido o icosaedro retroholorromo) es un poliedro uniforme estrellado, indexado como U72. Tiene 112 caras (100 triángulos y 12 pentagramas), 180 aristas y 60 vértices.​ Su símbolo de Schläfli es sr{⁵/₃,³/₂}.

Las 40 caras triangulares no procedentes del achatado componen 20 pares coplanarios, formando estrellas hexagonales que no son del todo regulares. A diferencia de la mayoría de los poliedros romos, posee simetrías de reflexión.

George Olshevsky lo apodó yog-sothoth (en honor a las deidades de los mitos de Cthulhu).​​

Envolvente convexa

Su envolvente convexa es un dodecaedro truncado no uniforme.


Dodecaedro truncado
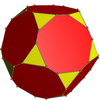Envolvente convexa
Pequeño icosicosidodecaedro retrorromo

Coordenadas cartesianas

Las coordenadas cartesianas de los vértices de un pequeño icosicosidodecaedro retrorromo son todas las permutaciones pares de:

(±(1-ϕ−α), 0, ±(3−ϕα))
(±(ϕ-1−α), ±2, ±(2ϕ-1−ϕα))
(±(ϕ+1−α), ±2(ϕ-1), ±(1−ϕα))

donde ϕ = (1+√5)/2 es el número áureo y α = √3ϕ−2.

Véase también

Referencias

  1. ↑ Maeder, Roman. «72: small retrosnub icosicosidodecahedron». MathConsult. 
  2. ↑ Birrell, Robert J. (May 1992). The Yog-sothoth: analysis and construction of the small inverted retrosnub icosicosidodecahedron (M.S.). California State University. 
  3. ↑ Bowers, Jonathan (2000). «Uniform Polychora». En Reza Sarhagi, ed. Bridges 2000. Bridges Conference. pp. 239-246. 

Enlaces externos