Tangente (geometría)

en verde: línea tangente
en azul: línea secante
en rojo: cuerda

La tangente a una curva en un punto P es una recta que toca a la curva solo en dicho punto, llamado punto de tangencia. Se puede decir que la tangente forma un ángulo nulo en dicho punto. Esta noción se puede generalizar desde la recta tangente a un círculo o una curva a figuras tangentes en dos dimensiones —es decir, figuras geométricas con un único punto de contacto (por ejemplo, la circunferencia inscrita)—, hasta los espacios tangentes, en donde se clasifica el concepto de tangencia en más dimensiones.

Geometría en el plano

Recta tangente a una curva

Una recta es tangente a una curva en un punto común si en dicho punto tiene la misma pendiente que la curva. La recta tangente es un caso particular de espacio tangente a una variedad diferenciable de dimensión 1, R 1 {\displaystyle \mathbb {R} ^{1}} $\mathbb {R} ^{1}$ . El problema pudo resolverse, planteando que tal recta es la posición límite de las rectas secantes de la curva que pasan por un punto fijo y los otros se acercan a tal punto. Una línea tangente simplemente toca una curva en un punto, coincidiendo con la pendiente de la curva allí. (Del latín tangens "tocar", como en la palabra "tangible").

Elaboración geométrica

Intuitivamente, la tangente TA es la posición límite del recto o el límite de las rectas secantes a la curva C, que pasan por los puntos A y Mi cuando se aproximan indefinidamente por M1, M2, M3, M4, …

Construcción analítica

Analíticamente, si C viene dada por una función f(x), tal que, A = ( a , f ( a ) ) {\displaystyle A=(a,f(a))} $A=(a,f(a))$ y M i = ( m i , f ( m i ) ) {\displaystyle M_{i}=(m_{i},f(m_{i}))} $M_{i}=(m_{i},f(m_{i}))$ , entonces la recta A M i {\displaystyle AM_{i}} $AM_{i}$ cuando lim i → ∞ m i = a {\displaystyle \lim _{i\to \infty }m_{i}=a} $\lim _{i\to \infty }m_{i}=a$ tendrá como coeficiente director o pendiente:

lim m i → a f ( m i ) − f ( a ) m i − a {\displaystyle \lim _{m_{i}\to a}{\frac {f(m_{i})-f(a)}{m_{i}-a}}}

\lim _{m_{i}\to a}{\frac {f(m_{i})-f(a)}{m_{i}-a}}

que por definición es f ′ ( a ) {\displaystyle f'(a)} $f'(a)$ la derivada de f en a.

La recta tangente, T A {\displaystyle T_{A}} $T_{A}$ , a la función es:

T A ( x ) = f ′ ( a ) ( x − a ) + f ( a ) {\displaystyle T_{A}(x)=f'(a)(x-a)+f(a)}

T_{A}(x)=f'(a)(x-a)+f(a)

Determinación de la recta tangente

Para determinar la recta tangente en un punto P(x,f(x)) basta con conocer su ángulo de inclinación, esto es:

lim Δ x → 0 ϕ ( Δ x ) = ϕ 0 {\displaystyle \lim _{\Delta x\to 0}{\phi (\Delta x)}=\phi _{0}}

\lim _{\Delta x\to 0}{\phi (\Delta x)}=\phi _{0}

Para hallar este ángulo se puede emplear su tangente trigonométrica, en otros términos la pendiente (inclinación angular) de la recta tangente. O sea:

lim Δ x → 0 ϕ ( Δ x ) = ϕ 0 {\displaystyle \lim _{\Delta x\to 0}{\phi (\Delta x)}=\phi _{0}}

\lim _{\Delta x\to 0}{\phi (\Delta x)}=\phi _{0}

t a n ϕ ( Δ x ) = Δ y Δ x {\displaystyle tan\phi (\Delta x)={\frac {\Delta y}{\Delta x}}}

tan\phi (\Delta x)={\frac {\Delta y}{\Delta x}}

t a n ϕ ( Δ x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x {\displaystyle tan\phi (\Delta x)=\lim _{\Delta x\to 0}{f(x+\Delta x)-f(x) \over \Delta x}}

tan\phi (\Delta x)=\lim _{\Delta x\to 0}{f(x+\Delta x)-f(x) \over \Delta x}

Si en el punto x existe la recta tangente (no vertical) a la curva entonces existe el límite

lim Δ x → 0 t a n ϕ ( Δ ) = lim Δ x → 0 Δ y Δ x = t a n ϕ 0 {\displaystyle \lim _{\Delta x\to 0}tan\phi (\Delta )=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=tan\phi _{0}}

\lim _{\Delta x\to 0}tan\phi (\Delta )=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=tan\phi _{0}

Por tanto, se puede obtener el ángulo ϕ 0 {\displaystyle \phi _{0}} $\phi _{0}$ como el arco tangente:

ϕ 0 = a r c t a n lim Δ x → 0 Δ y Δ x {\displaystyle \phi _{0}=arctan{\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}}}

\phi _{0}=arctan{\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}}

Finalmente, para la ecuación de la recta tangente, se necesita la pendiente m, que no es sino el límite lim Δ x → 0 Δ y Δ x {\displaystyle \lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}} $\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}$ , pues, además se conoce el punto de tangencia P(x, f(x)).

Circunferencias tangentes

Si se pone circunferencia de centro C i {\displaystyle C_{i}} $C_{i}$ y radio r i {\displaystyle r_{i}} $r_{i}$ , es tangente en un punto P {\displaystyle P} $P$ a otra circunferencia de centro C j {\displaystyle C_{j}} $C_{j}$ y radio r j {\displaystyle r_{j}} $r_{j}$ si el los dos centros de las circunferencias y el punto de tangencia están sobre la misma recta, y el punto P {\displaystyle P} $P$ de tangencia es la intersección de las dos circunferencias.

Así partiendo de una circunferencia y un punto P, de la misma, trazando una recta que pase por el centro de la circunferencia y el punto P, cualquier circunferencia con centro en esta recta, que pase por P, será tangente a la circunferencia dada en ese punto.

Circunferencia tangente a una recta

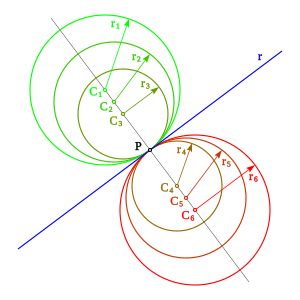
Dada una recta r y un punto P de la misma, trazando la perpendicular a la recta r por P, cualquier circunferencia con centro en esta perpendicular que pase por P es tangente a r en el punto P.

Por el razonamiento inverso podemos trazar la recta tangente a una circunferencia en un punto P dado. Su ecuación se llama ecuación de la desdoblada.

Plano tangente

En geometría diferencial, espacio tangente es el conjunto asociado a cada punto de una variedad diferenciable formado por todos los vectores tangentes a dicho punto. Es un espacio vectorial de la misma dimensión que la dimensión de la variedad.

Hay varias formas de entender este concepto. Primero vamos a explicar utilizando la gráfica de al lado. Empecemos suponiendo que tenemos una curva γ {\displaystyle \gamma } $\gamma$ en la variedad M que pasa por alguna posición elegida cualquiera: x ∈ M {\displaystyle x\in M} $x\in M$ . Es decir un mapeo γ : ] − ε , ε -\varepsilon ,\varepsilon -\varepsilon ,\varepsilon

Referencias

↑ Real Academia Española, 2001

Bibliografía

Hazewinkel, Michiel, ed. (2001), «Tangent_line&oldid=14413», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
Weisstein, Eric W. «Recta tangente». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

Enlaces externos

Recta tangente a una circunferencia, «El paraíso de las matemáticas», sitio interactivo.