Triángulo rectángulo

Apariencia mover a la barra lateral ocultar

En geometría, se denomina triángulo rectángulo a cualquier triángulo que tiene un ángulo recto, es decir, un ángulo de 90 grados. Las razones entre las longitudes de los lados de un triángulo rectángulo es un enfoque de la trigonometría plana. En particular, en un triángulo rectángulo, se cumple el llamado teorema de Pitágoras ya conocido por los babilonios, entre los años 2000 y 1600 a. C., en la Mesopotamia.

Terminología y casos especiales

Un triángulo rectángulo y sus elementos.

Se denomina hipotenusa al lado mayor del triángulo rectángulo y es el lado opuesto al ángulo recto. Se llaman catetos a los dos lados menores, los que conforman el ángulo recto; cada cateto se opone a un ángulo agudo. Sólo si la medida de los tres lados son números enteros, estos constituyen un trío de nombre terna pitagórica.

Si los catetos son iguales se llama triángulo rectángulo isósceles ( 45-90-45); siendo

0. sen ⁡ π 4 = cateto hipotenusa = 2 2 {\displaystyle \operatorname {sen} {\frac {\pi }{4}}={\frac {\text{cateto}}{\text{hipotenusa}}}={\frac {\sqrt {2}}{2}}} $\operatorname {sen} {\frac {\pi }{4}}={\frac {\text{cateto}}{\text{hipotenusa}}}={\frac {\sqrt {2}}{2}}$

Un triángulo rectángulo escaleno muy conocido, es el que tiene el cateto menor igual a la mitad de la hipotenusa, y estos dos lados forman un ángulo agudo de 30° y el otro ángulo de 60°, (30-90-60) y se obtiene al bisecar un triángulo equilátero por su altura; resultan estas razones entre dichos lados. Si admitimos que el lado del triángulo equilátero es 2 a {\displaystyle 2a} $2a$ y mediante una altura se obtienen dos triángulos rectángulos, tal que en cada uno la hipotenusa es 2 a {\displaystyle 2a} $2a$ ; cateto opuesto al ángulo de 30°, a {\displaystyle a} $a$ y cateto opuesto al ángulo de 60°, a 3 {\displaystyle a{\sqrt {3}}} $a{\sqrt {3}}$ , se obtienen los siguientes valores de los respectivos senos:

1. sen ⁡ π 6 = cateto menor hipotenusa = a 2 a = 1 2 {\displaystyle \operatorname {sen} {\frac {\pi }{6}}={\frac {\text{cateto menor}}{\text{hipotenusa}}}={\frac {a}{2a}}={\frac {1}{2}}} $\operatorname {sen} {\frac {\pi }{6}}={\frac {\text{cateto menor}}{\text{hipotenusa}}}={\frac {a}{2a}}={\frac {1}{2}}$

2. sen ⁡ π 3 = cateto mayor hipotenusa = a 3 2 a = 3 2 {\displaystyle \operatorname {sen} {\frac {\pi }{3}}={\frac {\text{cateto mayor}}{\text{hipotenusa}}}={\frac {a{\sqrt {3}}}{2a}}={\frac {\sqrt {3}}{2}}} $\operatorname {sen} {\frac {\pi }{3}}={\frac {\text{cateto mayor}}{\text{hipotenusa}}}={\frac {a{\sqrt {3}}}{2a}}={\frac {\sqrt {3}}{2}}$

Propiedades

En todo triángulo rectángulo se cumple que:

Tiene un ángulo recto (90°).
Tiene dos ángulos agudos que son complementarios, es decir, que la suma de ambos es de 90°.
La hipotenusa siempre es mayor que cualquiera de los catetos.
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
La suma de la longitud de la hipotenusa y el diámetro de un círculo inscrito en el triángulo es igual a la suma de la longitud de los catetos.
Para efectos de área, un cateto cualquiera se puede considerar como base y el otro cateto como altura.
La mediana de la hipotenusa descompone un triángulo rectángulo escaleno en dos triángulos: uno obtusángulo y otro acutángulo, no congruentes pero equivalentes.
La mediana de la hipotenusa de un triángulo rectángulo isósceles lo descompone en dos triángulos rectángulos isósceles congruentes y equivalentes
Dos triángulos rectángulos, con hipotenusa común, y los ángulos rectos en semiplanos opuestos determinados por la recta que contiene a la hipotenusa, forman un cuadrilátero birrectángulo.
La mediana que parte del ángulo recto es igual a la mitad de la hipotenusa.
La altura que parte del vértice del ángulo recto, coincide con un cateto, con tal de considerar al otro cateto como una base.

Tipos de triángulo rectángulo

Existen dos tipos de triángulo rectángulo:

Triángulo rectángulo isósceles: los dos catetos son de la misma longitud, los ángulos interiores son de 45-45-90. En este tipo de triángulo, la hipotenusa mide 2 {\displaystyle {\sqrt {2}}} ${\sqrt {2}}$ veces la longitud del cateto.

Triángulo rectángulo escaleno: los tres lados y los tres ángulos tienen diferente medida. Un caso particular es aquel cuyos ángulos interiores miden 30-60-90, en este tipo de triángulo, la hipotenusa mide el doble del cateto menor, y el cateto mayor 3 {\displaystyle {\sqrt {3}}} ${\sqrt {3}}$ veces la longitud del cateto menor.

Triángulo rectángulo isósceles.
Triángulo rectángulo escaleno.

Triángulo rectángulo de lados consecutivos: las medidas de sus lados tienen 3, 4 y 5 unidades de longitud. Aparece en las culturas del cercano oriente: Babilonia y Egipto. Histórico, útil y didáctico, adaptable a un geoplano. Sin lados consecutivos es el triángulo de lados que miden 5,12 y 13 unidades de longitud, menos conocido que el anterior.

Relaciones métricas

Las relaciones métricas del triángulo rectángulo son cuatro. Los tres triángulos formados al trazar la altura relativa a la hipotenusa son rectángulos y semejantes.

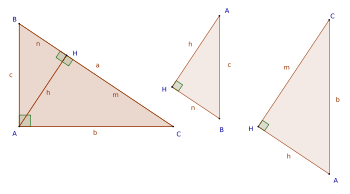Ilustración de los principales elementos del triángulo rectángulo:
a es la hipotenusa,
b el cateto mayor,
c el cateto menor,
h la altura relativa a la hipotenusa,
m la proyección del cateto b y
n la proyección del cateto c.

La hipotenusa es igual a la suma de las proyecciones.

a = m + n {\displaystyle a=m+n\,\!}

a=m+n\,\!

Por semejanza de triángulos, tenemos que:

El cuadrado de la altura relativa de los catetos.

h m = n h ⇒ h 2 = m n {\displaystyle {\frac {h}{m}}={\frac {n}{h}}\Rightarrow h^{2}=mn\,\!}

{\frac {h}{m}}={\frac {n}{h}}\Rightarrow h^{2}=mn\,\!

El cuadrado de un cateto, es igual al producto entre su proyección (que se encuentra de su lado) y la hipotenusa.

b a = m b ⇒ b 2 = a m {\displaystyle {\frac {b}{a}}={\frac {m}{b}}\Rightarrow b^{2}=am\,\ }

{\frac {b}{a}}={\frac {m}{b}}\Rightarrow b^{2}=am\,\

c a = n c ⇒ c 2 = a n {\displaystyle {\frac {c}{a}}={\frac {n}{c}}\Rightarrow c^{2}=an\,\ }

{\frac {c}{a}}={\frac {n}{c}}\Rightarrow c^{2}=an\,\

El producto entre la hipotenusa y la altura relativa a ella, es igual al producto de los catetos.

a c = b h ⇒ a h = b c {\displaystyle {\frac {a}{c}}={\frac {b}{h}}\Rightarrow ah=bc\,\ }

{\frac {a}{c}}={\frac {b}{h}}\Rightarrow ah=bc\,\

Teorema de Pitágoras

El teorema de Pitágoras establece que:

En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

a 2 + b 2 = c 2 {\displaystyle \displaystyle a^{2}+b^{2}=c^{2}}

\displaystyle a^{2}+b^{2}=c^{2}

Fórmulas para calcular un lado desconocido en función de los otros dos, donde a y b son los catetos y c es la hipotenusa.

a = c 2 − b 2 {\displaystyle a={\sqrt {c^{2}-b^{2}}}}

a={\sqrt {c^{2}-b^{2}}}

b = c 2 − a 2 {\displaystyle b={\sqrt {c^{2}-a^{2}}}}

b={\sqrt {c^{2}-a^{2}}}

c = a 2 + b 2 {\displaystyle c={\sqrt {a^{2}+b^{2}}}}

c={\sqrt {a^{2}+b^{2}}}

Teorema de la altura

El teorema de "la altura de un triángulo rectángulo" establece que:

Teorema de la altura (forma 1)

En cualquier triángulo rectángulo la altura relativa a la hipotenusa es la media geométrica entre las proyecciones ortogonales de los catetos sobre la hipotenusa.

Demostración

La altura del triángulo rectángulo ABC (véase Figura 1) lo divide en dos triángulos rectángulos semejantes, de forma que

h n = m h {\displaystyle {\frac {h}{n}}={\frac {m}{h}}}

{\frac {h}{n}}={\frac {m}{h}}

Figura 1: Teorema de la altura.

Multiplicando los dos miembros de la igualdad por h n {\displaystyle hn} $hn$ se tiene:

h 2 = m n {\displaystyle h^{2}=m\,n\,}

h^{2}=m\,n\,

por lo que

(1) h = m n {\displaystyle h={\sqrt {m\,n}}} $h={\sqrt {m\,n}}$

Otra forma del mismo teorema

La altura h correspondiente a la hipotenusa de un triángulo rectángulo (véase Figura 1) también puede obtenerse reemplazando a los valores m y n de la ecuación (1) del presente teorema por sus respectivos equivalentes dados por el teorema del cateto.

m = b 2 a {\displaystyle m={\frac {b^{2}}{a}}\,}

m={\frac {b^{2}}{a}}\,

; n = c 2 a {\displaystyle n={\frac {c^{2}}{a}}\,}

n={\frac {c^{2}}{a}}\,

(h2) h = m n = b 2 a c 2 a {\displaystyle h={\sqrt {m\,n}}={\sqrt {{\frac {b^{2}}{a}}{\frac {c^{2}}{a}}}}} $h={\sqrt {m\,n}}={\sqrt {{\frac {b^{2}}{a}}{\frac {c^{2}}{a}}}}$

lo que al simplificar en el último término de la ecuación (h2) la raíz con los cuadrados nos conduce a:

(h3) h = b c a {\displaystyle h={\frac {b\,c}{a}}} $h={\frac {b\,c}{a}}$

Donde h es la altura (relativa a la hipotenusa), b y c los catetos y a la hipotenusa.

La ecuación (h3) nos permite establecer el enunciado (forma 2) del teorema:

Teorema de la altura (forma 2)

En todo triángulo rectángulo la altura h (relativa a la hipotenusa) es igual al producto de sus catetos b y c divididos por la hipotenusa a.

Teorema del cateto

El teorema del cateto establece lo siguiente:

Teorema del cateto

En todo triángulo rectángulo el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección ortogonal de ese cateto sobre la hipotenusa.

Este teorema (véase Figura 1) puede expresarse matemáticamente —para cada uno de sus dos catetos— como:

b 2 = c m {\displaystyle b^{2}\ =\ c\;m} $b^{2}\ =\ c\;m$

a 2 = c n {\displaystyle a^{2}\ =\ c\;n} $a^{2}\ =\ c\;n$

Donde m y n son, respectivamente, las proyecciones de los catetos b y a sobre la hipotenusa c.

Demostración

Figura 1 - Los segmentos m y n son las respectivas proyecciones de los lados b y a sobre la hipotenusa c, siendo h la altura correspondiente a la hipotenusa.

Sea el triángulo ΔABC rectángulo en C, dispuesto de modo que su base es la hipotenusa c. La altura h determina los segmentos m y n, que son, respectivamente, las proyecciones de los catetos b y a sobre la hipotenusa.

Los triángulos rectángulos ΔABC, ΔACH y ΔCBH tienen iguales sus ángulos, y por lo tanto son semejantes:

Todos tienen un ángulo recto.
Los ángulos B y ACH son iguales por ser agudos, por abarcar un mismo arco, y tener sus lados perpendiculares.
Igualmente sucede con los ángulos A y CBH.

Puesto que en las figuras semejantes los lados homólogos son proporcionales, tendremos que:

Por la semejanza entre los triángulos ΔACH y ΔABC

b m = c b {\displaystyle {\frac {b}{m}}={\frac {c}{b}}}

{\frac {b}{m}}={\frac {c}{b}}

de donde,

b 2 = c m {\displaystyle b^{2}\ =\ cm}

b^{2}\ =\ cm

Por la semejanza entre los triángulos ΔCBH y ΔABC

a n = c a {\displaystyle {\frac {a}{n}}={\frac {c}{a}}}

{\frac {a}{n}}={\frac {c}{a}}

a 2 = c n {\displaystyle a^{2}\ =\ cn}

a^{2}\ =\ cn

y el teorema queda demostrado.

Corolario

“En todo triángulo rectángulo la longitud de la proyección ortogonal de cualquier cateto sobre la hipotenusa es igual al cuadrado de la longitud de ese mismo cateto dividido por la longitud de la hipotenusa.”

Basados en las dos ecuaciones del teorema anterior, para deducir el «corolario 1» basta con despejar en cada una de ellas, la respectiva variable de su proyección ortogonal, siendo éstas m y n:

b 2 = c m ; a 2 = c n {\displaystyle b^{2}\ =\ c\;m\;\;\;\;;\;\;\;\;a^{2}\ =\ c\;n} $b^{2}\ =\ c\;m\;\;\;\;;\;\;\;\;a^{2}\ =\ c\;n$

en las que al despejar respectivamente m y n producen las ecuaciones del «corolario 1»:

m = b 2 c ; n = a 2 c {\displaystyle m={\frac {b^{2}}{c}}\;\;\;\;;\;\;\;\;n={\frac {a^{2}}{c}}} $m={\frac {b^{2}}{c}}\;\;\;\;;\;\;\;\;n={\frac {a^{2}}{c}}$

donde m es la proyección ortogonal del cateto b sobre la hipotenusa c (véase figura 1) y n es la proyección ortogonal del cateto a también sobre la hipotenusa c.

Un triángulo rectángulo puede dividirse en dos triángulos rectángulos, obteniendo tres triángulos semejantes entre sí (el original y los dos divididos). Para esto, la medida de cada cateto es media proporcional entre la medida de la hipotenusa y la medida de la proyección de éste sobre ella.

a b = b m {\displaystyle {\frac {a}{b}}={\frac {b}{m}}} ${\frac {a}{b}}={\frac {b}{m}}$ , también se cumple: a c = c n {\displaystyle {\frac {a}{c}}={\frac {c}{n}}} ${\frac {a}{c}}={\frac {c}{n}}$

La medida de la altura es media proporcional entre los dos segmentos que determina sobre la hipotenusa.

m h = h n {\displaystyle {\frac {m}{h}}={\frac {h}{n}}} ${\frac {m}{h}}={\frac {h}{n}}$ , es decir: h 2 = m ⋅ n {\displaystyle h^{2}=m\cdot n\,} $h^{2}=m\cdot n\,$

Las tres alturas del triángulo rectángulo pueden calcularse como:

h a = b ⋅ c a {\displaystyle h_{a}={\frac {b\cdot c}{a}}} $h_{a}={\frac {b\cdot c}{a}}$ ; h b = c {\displaystyle h_{b}=c} $h_{b}=c$ ; h c = b {\displaystyle h_{c}=b} $h_{c}=b$

donde b y c son los catetos y a, la hipotenusa, en tanto que ha, hb y hc son las alturas sobre los respectivos lados.

Razones trigonométricas

En un triángulo rectángulo, las razones trigonométricas del ángulo, con vértice en 'A, con medida α {\displaystyle \alpha \;} $\alpha \;$ ', son:

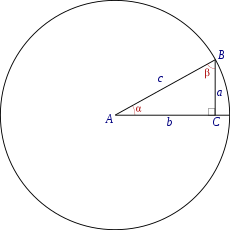
El seno: la razón entre el cateto opuesto y la hipotenusa,

sen ( α ) = a c {\displaystyle {\text{sen}}(\alpha )={\frac {a}{c}}}

{\text{sen}}(\alpha )={\frac {a}{c}}

; su inverso multiplicativo, si existe, se denomina cosecante

El coseno: la razón entre el cateto adyacente y la hipotenusa,

cos ⁡ ( α ) = b c {\displaystyle \cos(\alpha )={\frac {b}{c}}}

\cos(\alpha )={\frac {b}{c}}

; su inverso multiplicativo si existe, se llama secante.

La tangente: la razón entre el cateto opuesto y el adyacente,

tan ⁡ ( α ) = a b {\displaystyle \tan(\alpha )={\frac {a}{b}}}

\tan(\alpha )={\frac {a}{b}}

; el inverso de la razón anterior, si es posible, se nombra cotangente.

Área

fig. ar1: Relación entre el rectángulo y dos de las tres alturas (la de los catetos) de un triángulo rectángulo.

Se puede considerar el área de un triángulo rectángulo como la mitad del área de un rectángulo partido por su diagonal, véase fig. ar1, (o un cuadrado si el triángulo rectángulo es además isósceles).

(A1) A = b ⋅ a 2 {\displaystyle A={\frac {b\cdot a}{2}}} $A={\frac {b\cdot a}{2}}$

donde a y b de la ecuación (A1) representan las medidas de los dos catetos que coinciden con los dos lados y las correspondientes alturas del rectángulo (véase fig. ar1).

En todo triángulo rectángulo cada uno de los dos catetos es siempre la respectiva altura del otro. Asumiendo que a = cateto1 y b = cateto2 se puede escribir una versión equivalente de ecuación (A1) de la siguiente manera:

A = c a t e t o 1 ⋅ c a t e t o 2 2 {\displaystyle A={\frac {cateto1\cdot cateto2}{2}}} $A={\frac {cateto1\cdot cateto2}{2}}$

La demostración anterior es solo un caso especial, restringido, de una mucho más general que vale para todo triángulo (no solo para los triángulos rectángulos); Y esta es la "proposición I.41 de Euclides, la cual se basa en el concepto más general de paralelogramo y no se restringe al rectángulo. Dicha proposición I.41 extiende la validez de la ecuación (A1) a todo triángulo.

Área máxima

El triángulo rectángulo de mayor área que se puede inscribir en una semicircunferencia es el triángulo rectángulo isósceles, es decir, el que tiene los catetos iguales y de longitud R 2 {\displaystyle R{\sqrt {2}}} $R{\sqrt {2}}$ donde R es el radio de la semicircunferencia circunscrita y la hipotenusa coincide con el diámetro.

Demostración
Trabajando sobre la semicircunferencia y usando la función área A ( x ) = ( 2 R ) ( h ) 2 {\displaystyle A(x)={\frac {(2R)(h)}{2}}} $A(x)={\frac {(2R)(h)}{2}}$ donde la base tomada es la hipotenusa y la altura es perpendicular a la misma. Entonces claramente A(x) es máxima cuando h sea máximo, ya que 2R es constante; como el máximo valor de h se obtiene sobre la semicircunferencia cuando h=R se tiene por simetría que el triángulo rectángulo es isósceles.

En tres dimensiones

Un triángulo rectángulo que gira, teniendo como eje uno de sus catetos y como generatriz su hipotenusa, genera un cono de radio igual el cateto no axial y altura igual al cateto axial.

Si dos triángulos rectángulos semejantes engendran dos conos, en las condiciones del enunciado precedente, entonces sus volúmenes son proporcionales a los cubos de cualquier par de lados correspondientes. También las áreas son proporcionales a los cuadrados de cualquier par de lados correspondientes.

Si ambos conos tienen el mismo eje, y un plano secante que interseca ambos conos genera dos elipses, dichas elipses tienen ejes proporcionales entre sí (es decir, son semejantes).

Véase también

Referencias

↑ Weisstein, Eric W. «Triángulo rectángulo». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. .(Cita DRAE|Triángulo|Triángulo rectángulo})}
↑ Hofmann: "Historia Texto en negritade la Matemática" (2003), Limusa Noriega Editores, México, D.F. pg. 11
↑ A. V. Pogorélov «Geometría elemental»
↑ Nichols. Palmer. Schacht: Geometría Moderna, Cecsa México décimo tercera impresión (1989)
↑ Comprobable directamente, sobre la base de la definición de mediana, etc
↑ Benítez. «Geometría plana»
↑ Esta nota se basa en Matemáticas, publicación de la revista Life
↑ «Que significa teorema del cateto en Matemáticas».
↑ «Teorema del cateto».
↑ Álgebra y trigonometría con geometría analítica ISBN 968-880-222-0
↑ Euclides Los Elementos, proposición I.41 → "Si un paralelogramo tiene la misma base que un triángulo y está contenido entre las mismas paralelas, el paralelogramo es el doble del triángulo".
↑ Stanley Clemens; Phares O'Daffer; Thomas J Cooney (1984). Geometria Con Aplicaciones Y Solución De Problemas. Addison Wesley. ISBN 0-201-64407-X.

Enlaces externos

Wikimedia Commons alberga una categoría multimedia sobre Triángulo rectángulo.
Teorema de Gudea: Triángulos rectángulos sin raíces cuadradas
Sitio web: Disfruta las matemáticas .